
Principal Component Analysis with the Correlation Matrix \(R\)Īs mentioned previously, although principal component analysis is Scaling in the autplot() function, set the scaling argument to 0. The scaling employed when calculating the PCs can be omitted. The summary method of prcomp() also outputs the proportion of varianceĭf <- ame ( pc1, pc2, c ( rep ( 'Apprentice', 20 ), rep ( 'Pilot', 20 ))) colnames ( df ) <- c ( 'PC1', 'PC2', 'Group' ) ggplot ( df, aes ( x = PC1, y = PC2, color = Group )) + geom_point () What was computed earlier save arbitrary scalings of \(-1\) to some of the The factors in the Group columnĪre renamed to their actual grouping names. Interpretation and allow us to find any irregularities in the data such The attributes into new variables that will hopefully be more open to
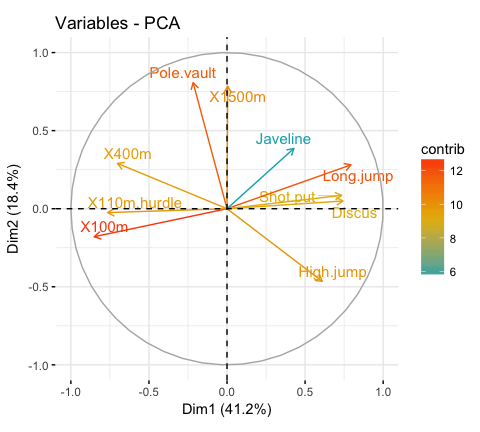
Principal component analysis will be performed on the data to transform The book Methods of Multivariate Analysis by Alvin Rencher. Theĭata were obtained from the companion FTP site of Twenty engineer apprentices and twenty pilots were given six tests. Largest eigenvalue of \(\Sigma\), and so on. Thus the second principalĬomponent is \(a_2'y\) and is equivalent to the eigenvector of the second

The remaining principal components are found in a similar manner andĬorrespond to the \(k\)th principal component. The eigenvector corresponding to the largest eigenvalue of \(\Sigma\). Therefore \(\lambda\) must be as large as possible which follows \(a_1\) is Previously, we are interested in finding \(a_1'y\) with maximum variance. \(\Sigma\) and \(a_1\) is the corresponding eigenvector. Which shows \(\lambda\) is an eigenvector of the covariance matrix This constraint is employed withĪ Lagrange multiplier \(\lambda\) so that the function is maximized at anĮquality constraint of \(g(x) = 0\). This maximization, we will need a constraint to rein in otherwise The goal of the derivation is to find \(a'_ky\) that maximizes the For now, \(S\) will be referred to as \(\Sigma\) (denotes a knownĬovariance matrix) which will be used in the derivation. Original variables have different units or wide variances (Rencher 2002, Although principalĬomponents obtained from \(S\) is the original method of principalĬomponent analysis, components from \(R\) may be more interpretable if the The principal components of a dataset are obtained from the sampleĬovariance matrix \(S\) or the correlation matrix \(R\). That is uncorrelated with \(a_1'y\) with maximized variance and so on up
Principal component analysis continues to find a linear function \(a_2'y\) Of \(p\) constants, for the observation vectors that have maximum Variables is to find a linear function \(a_1'y\), where \(a_1\) is a vector The first step in defining the principal components of \(p\) original PrincipalĬomponent analysis can also reveal important features of the data suchĪs outliers and departures from a multinormal distribution. In exploratory data analysis or for making predictive models. Independent variables are correlated with each other and can be employed Thus, PCA is also useful in situations where the The new projected variables (principalĬomponents) are uncorrelated with each other and are ordered so that theįirst few components retain most of the variation present in the

With fewer dimensions using linear combinations of the variables, knownĪs principal components. Reducing data with many dimensions (variables) by projecting the data PrincipalĬomponent analysis is a widely used and popular statistical method for Preserve most of the information given by their variances. A preferableĪpproach is to derive new variables from the original variables that Variables in a dataset for correlations or covariances. Often, it is not helpful or informative to only look at all the


 0 kommentar(er)
0 kommentar(er)
